|
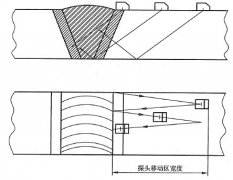
相对于板、棒和管等简单结构工件,较容易实现超声检测;但对于结构由两种或两种以上的简单结构组成的复杂工件,一般都具有几何形状复杂和棱边多的特点,这给超声探伤方法的选择及信号处理带来困难。本文的研究对象为一种轻质材料异形工件,其结构如图1所示,右端为实心圆柱,左端为梅花内孔的薄壁管,管内壁等间隔分布有六个轴向圆弧槽,管外径Φ40.5mm,壁最薄处厚度为4.6mm,最厚处为6.0mm。其结构复杂且承压受力,是整个工件检测的重点和难点。
该工件左端梅花内孔经多次热处理和冷挤压工艺成型,产生裂纹类缺陷如图2所示,在使用常规方法纯横波探伤时,由于孔内棱边强烈的回波反射,湮灭了缺陷回波而无法人工识别。因此本文将论述如何使用爬波技术及信号处理方法实现检测。
1.png
图2 工件内壁裂纹缺陷
1.爬波检测原理
1.1 爬波的产生条件
根据几何声学原理和Snell定律可知,当超声纵波从一种介质以一定角度倾斜入射到另一种介质表面时,就会发生反射和折射现象,同时还伴有波型转换,会在第二种介质中产生折射纵波和折射横波[1]。如果入射波声速与折射波声速满足下列关系时:
C1L<C2T<C2L (式1-1)
式中:C1L是入射纵波在第一种介质中的纵波声速;
C2L 是入射纵波在第二种介质中的折射纵波声速;
C2T是入射纵波在第二种介质中的折射横波声速;
即超声波从声速小的介质(水)入射到声速大的介质(钢)时,随着入射角的增大,折射角也增大。当入射角α=arcsin(C1L/C2L)时,折射纵波将沿两种介质分界面传播,即纵波在第二种介质中的纵波折射角等于90°,此时α称为第一临界角。一般认为当入射角等于第一临界角时,就会在第二种介质的近表面下激发爬波,如图3所示。
1.2 爬波的特性
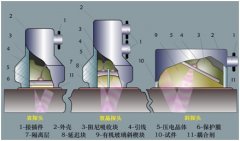
当纵波以第一临界角入射时,折射纵波的折射角为90°,沿第二种介质表面传播。由于受边界条件的约束,折射纵波在沿表面向前传播时会不断地向下辐射出斜射横波。我们把沿介质表面下一定距离处在横波与折射纵波之间传播的辐射横波峰值波称为爬波,把辐射横波的波前称为头波。可见,此时在第二种介质的近表面处的声场具有多波型的特征[2]。在入射点固定不动时,爬波的辐射点是固定的,从入射点附近向下辐射;头波的辐射点是不固定的,而是随着爬波的传播过程移动,不断地从爬波所在点向周围辐射。另外,根据波动声学理论分析可知,爬波是入射角等于第一临界角时的折射纵波与横波的合成。爬波引起的质点振动是纵波和横波的合成[3],此时质点的位移可用式1-2表示:
1.png (式1-2)
式中φ和是折射纵波和横波的势函数。
爬波具有如下特点[4]:
(1) 爬波的传播速度接近于折射纵波,其它条件相同时,其速度和波长都较大,故表面散射相对较弱,对表面粗糙度不敏感。(2) 折射纵波由于受到边界条件的约束会不断地向下辐射横波产生头波,且产生的头波具有相当的强度。因此爬波在离开探头后衰减很快,故只对近表面处缺陷敏感,适合检测薄件。(3) 爬波的最大幅值方向与表面有一个小的夹角,且与入射角有关,爬波主瓣(幅值最大值) 所对应的折射角θmax和入射角α关系如图4所示[5],可见随着入射角α的增加,主瓣对应的折射角θmax也在增大。因此适当调整纵波的入射角可以改变爬波在材料内部的主能量的方向,使反射回波的灵敏度最佳。(4) 爬波的能量主要集中在材料表面附近,但极大值并不沿表面传播而是与表面成一定角度,因此爬波可以检测材料近表面区域内的缺陷,最深可探测离表面10mm以内的缺陷。
2.检测技术及信号处理方法
检测用的标准样件,在外表面及内弧顶处分别刻有深度0.10mm长度8mm的纵向标准伤。采用水浸聚焦法在工件壁内激发爬波,检测原理如图5。首先将探头的入射角调整到第一临界角处,在工件壁内激发爬波,旋转工件使得外表面伤位于入射点附近,可以观察到很强的回波。然后适当调整入射角,观察弧顶伤回波信号,使回波信号有较高的灵敏度与分辨率。当工件旋转时,爬波就可以沿工件表面做周向扫查。图6显示了外表面与内弧顶处标准伤回波及棱边回波特性。
从图6中可看出各回波信号已接近饱和且相对于水钢界面波在时间上分辨率较好,能够从外到内清晰分辨出外表面伤回波、内弧顶伤回波及内棱边回波,说明爬波检测技术完全适合于本文研究对象的检测。相对于水钢界面波,外表面伤回波时间差最小,内棱边回波的时间差最大,内弧顶伤回波时间差居中。从波形相邻性来看,外表面伤回波与水钢界面波相邻而且时间上可分离,内弧顶伤回波与内棱边回波相邻且在时间上部分重叠,从时间上二者不可分离,也就是人工探伤无法分辨缺陷回波与棱边回波。
由于内弧顶处是整个工件的最薄处,因此弧顶处的缺陷是最致命的。为了保证弧顶缺陷不被漏检,在设置闸门时,将闸门前沿设置在水钢界面波与外表面伤回波中间,闸门后沿设置在内棱边回波主峰处,即只保留内棱边回波能量的一半,以保证弧顶伤及壁内较大的缺陷能够被捕获。动态跟踪闸门内回波信号峰值获得检测信号如图7所示,图7(a)是对标准样件(转速300转/min,检测螺距0.8mm)进行动态检测获得的峰值包络信号,图中标准伤回波包均已使用圆圈做了标注。
从图中可以明显地看出工件结构对超声波造成的影响:动态峰值信号以6个波包为一个周期,对应工件旋转一圈,每隔5个内棱边回波包出现一个标准伤回波包信号。图7(b)是一段不包含伤信号的内棱边回波包信号。从图7(a)中可以看出伤回波包信号与内棱边回波包信号在幅度上并没有明显差异,但是周期及面积则完全不同,标准伤信号的回波包面积要比内棱边回波包大,说明伤的反射要比工件内棱边反射强,而内棱边回波包信号的周期小(转动一圈会出现六个波包)且波包窄,二者主要差异体现为能量不同。因此,为有效抑制内棱边回波,本文根据二者的能量差异,提出一种滑窗平均能量补偿算法来实现对标准伤信号的有效提取。
其中,最主要的核心算法为滑窗平均,即以当前采样点为中心向前后各扩展N点,将这2N+1个点的数据相加后求平均作为当前点新的数据,对数据序列x[n]的索引遍历后获得一组新的数据y[n],公式如下:
式中每次滑动窗宽度为M=2N+1,y[n]为计算结果。这样的处理相当于加入一个低通滤波器,可以有效地抑制窄脉冲信号而平滑宽脉冲信号,正好满足对内棱边回波的抑制,虽然对标准伤回波会有一定的损失,通过适当的补偿算法可以在去除内棱边回波的情况下恢复出完整的伤回波。如图8所示,图8(a)中信号为图7(a)消除内棱边回波后恢复出干净的标准伤回波,而图8(b)则是无伤时消除内棱边回波后的信号时基线。
经过恢复的标准伤回波包信号具有明显的螺旋扫描幅度特征与大周期(一圈一个波包)特征,提高了回波信号信噪比,对该波包信号可使用阈值判伤等经典缺陷处理方法进行后续识别处理。
3.结论
|

 手机版
手机版