|
极限灵敏度为λ/2理论成立吗?
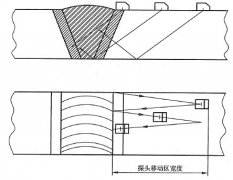
首先将CSK-IIIA试块平倒放在桌面上,φ1×6的小孔朝下,采用2个不同厂家生产的2.5MHz、φ20直探头(半波长约1.18mm)扫查φ1的平底孔。
试验结果如下图,将仪器的增益增加一定值时,两个探头检测φ1平底孔的反射回波均在仪器中显示,且远远大于噪声波高的6dB,则视为φ1平底孔可以被检测出来。
由此看来,小于λ/2的平底孔能被检测出来。岂不是教材中的理论知识脱离了实际,难道教材也有不严谨之处?
并非教材不是不严谨,而是确确实实的存在错误的认识!
教材会出错?不可能吧?这可不是我为了博大家的眼球而瞎造谣,造谣是犯法的,给我一百个胆子也不敢啊。
中国科学院声学研究所,沈建中教授在《超声探伤灵敏度与灵敏度上限》文中用白纸黑字反驳该理论。
沈教授认为超声检测的灵敏度确实是有上限的,但并不存在所谓的半波长超声探伤极限灵敏度。
通常只要缺陷的回波大于噪声6dB,则视为可以被检出,此时的灵敏度为上限。在常规超声检测中,仪器和探头组合性能、被检材质特性、缺陷类型等因素的组合信噪比是影响极限灵敏度的主要原因,并非是波长的一半。当检测系统的信噪较高时,被检出的缺陷可能是λ/2、λ/3、λ/4、λ/5……甚至更小。
用什么方式证明半波长极限灵敏度是错误的呢?
常规超声检测是通过探测由缺陷产生的散射超声波信号来检测缺陷,其中脉冲反射法中所接收的是缺陷背散射超声波信号。在许多教材中,超声散射常作为噪声的来源和信号能量损失的原因。但是,超声散射首先是超声检测的基础。
相关理论模型表明:无论缺陷多小,总是有背散射波反射到探头。返回信号的强弱与缺陷大小、超声波长、缺陷深度均存在一定的数学关系式,但与半波长并不存在直接的关系。只要缺陷散射波大于系统的噪声,它就可能被探测到。
从该理论模型可以看出,信噪比才是影响探伤灵敏度上限的主要因素,而非波长。
教材中提到:选用高频探头,可以提高检测灵敏度。难道不是为了减小超声波波长,使λ/2更小,从而提高检测灵敏度吗?
教材中提到增加频率,可以提高检测灵敏度,往往由于自己错误的认识认为增加频率,超声波的波长(λ=c/f)越短高,检测中能够识别最小缺陷的能力越强,极限灵敏度也越高。这种理解看似有理,却非正确的推断。
相关理论表明:散射的强度与频率有关,(1)当缺陷远大于波长λ时,几乎与工作频率无关,主要产生反射波;(2)当缺陷大小接近波长λ时,散射与频率关系复杂,有时变大、有时变小;(3)当缺陷远小于波长λ时,散射随频率的n次幂增长。
由此看来,当检测小缺陷时,可以适当增加频率,达到提高检测灵敏度的目的。但不是为了减小λ/2,以至于提高检测灵敏度。并且不能无限制的增加频率,频率过大,会造成声束能量衰减严重,降低信噪比,会降低检测灵敏度。
下图是两个不同频率的探头对φ1平底孔的反射回波比较,可以看出5MHz比2.5MHz的信噪比高。因此,增加频率,确实可以提高检测灵敏度。
最后一个问题:为什么将极限灵敏度λ/2写进教材呢?
关于这个问题我与“粉丝”经过深入探讨,我们曾以为极限灵敏度λ/2正确的前题,是基于理想情况下存在的。
什么是理想情况呢?比如:超声教材中很多公式和原理都是基于连续波——正弦波、余弦波——推导出来的,实际上我们使用的超声并非连续波而是脉冲波,脉冲波是由许多不同频率的连续波通过傅里叶变换合成的,所以脉冲波有别于连续波。
当缺陷大小接近半波长时,连续波可能会发生完全衍射,导致缺陷无反射回波。而脉冲波由多种频率组成,频率具有一定的带宽,那么波长也将存在一定的带宽。我们推测当中心频率的一半波长与缺陷尺寸相同时,会发生全衍射,其他波长不发生全衍射,这就是为什么当缺陷尺寸接近脉冲波的半波长时仍然也有回波的原因。
但是我查阅了许多文献,并未找到能证明连续波会发生全部衍射的证据。而是当障碍物接近波长一半时,衍射现象很明显,但没有全衍射概念。因此,上面的推测应该是不成立的。
沈教授认为:对于常规超声波探伤来说,其检测分辨力存在理论极限值,它是工作波长的一半。而对检测限灵敏度λ/2的错误结论,也许是混淆了检测灵敏度和检测分辨力造成的。
当然这些仅是我个人的理解和观点,欢迎在留言中提出不同的看法。
|

 手机版
手机版